Introduction to Velocity, its definition, Formula and examples:

In physics, velocity is a very special entity that, while it may not appear to be particularly important, is the most fundamental concept. The quantity of energy contained within a body as a result of its motion is defined as its velocity. So, if a body moves away from its beginning position at its own pace as time passes, we say the body has gained velocity.

It plays a role when conservative forces such as gravitational force, electromagnetic force, and nuclear force (basic forces of nature) are operating on a body and when vector addition is required because, unlike speed, velocity is a vector quantity.

Which is determined by the shortest distance travelled rather than the overall distance travelled. This is one of the fascinating aspects of our fundamental forces of nature.

Imagine calculating the velocity of a stone hurled from a specific height. It cannot be calculated using standard speed formulae! You'd need its vector form, i.e., velocity!

Definition

Wikipedia states that

“The velocity of an object is the rate of change of its position with respect to a frame of reference, and is a function of time.”

OR

"Velocity is the amount of distance a body moves in a given direction in a given length of time."

OR

"Speed refers back to the charge at which displacement changes."

OR

"Velocity" means "speed in a specific direction."

Formula

The equation used to locate velocity is given as

Velocity = Displacement / Time

OR

v = d / t

Where d is the displacement or distance, t is the time elapsed, and v is the body's velocity.

SI unit

In system international velocity is measured in meter per second (ms^-1). A body's velocity is one metre per second if it covers one metre in one second when a net force is applied to it.

Dimensions

As we know that

Velocity = Displacement / Time

OR

v = d / t

[v] = [d] / [t]

[v] = L¹ M ⁰ T⁰ / L⁰ M ⁰ T¹

[v] = L¹ M ⁰ T^-1

So velocity have dimensional formula is equal to [v] = L¹ M ⁰ T^-1

Difference between speed and velocity

Speed and velocity are two distinct quantities that can be compared as follows:

• Speed is the overall distance travelled by a body in a certain time interval, whereas velocity is the entire movement of the body in the same time span.
• Speed is a scaler quantity, whereas velocity is a vector quantity (scalar quantities have only magnitude, whereas vector quantities have magnitude as well as a specific direction OR only those quantities that follow triangle law of addition or parallelogram law of addition are called vector quantities).
• For example, if a body moves from west to east 40 m and then from east to north 30 m in 10 seconds, the total distance covered is 70m and the total time taken is 10 seconds, so speed would be distance upon time, i.e. 7 m/sec, but for speed the total displacement could be determined by Pythagoras theorem as a base is 40m and height is 30 m, so hypotenuse would be 50m, displacement would be 50 m.

Why we need velocity

We are all aware that knowledge on an object's motion is useful for analysing its motion. The amount and direction of a body's motion are specified by two parameters. Any physical quantity's magnitude is its numerical value represented in proper units.

The magnitude of an object's velocity makes studying it impossible. It is also necessary to consider the directions in which a body moves.

It makes little sense, for example, to simply state that the body is moving; it is far better to state that the body is moving but in a certain direction. So a body's speed just tells us about the amount of motion, whereas velocity tells us about the magnitude as well as the direction of motion.

How to calculate the problems of Velocity?

Example 1:

What is the velocity of a moving vehicle on a route that travels 400 metres in five seconds?

Solution: Manual method

Step 1: write given data values

Distance = d = 400m

Time taken = t =5s

Velocity = v =?

Step 2: Write general formula for net force

v = d / t

Step 3: Put the given data values

v = 400m / 5s

v = 80m/s

Hence the velocity of vehicle is 66.66m/s.

A velocity calculator can also be used to solve the above problem. It enables us to use velocity to address challenges quickly and effectively.

It divides the complexity into manageable chunks, allowing students to devote more time to learning the subject. The approaches indicated below can be used to solve the problems.

Solution: Using velocity calculator

Step 1: Choose the sentence you want to calculate from the drop-down menu.

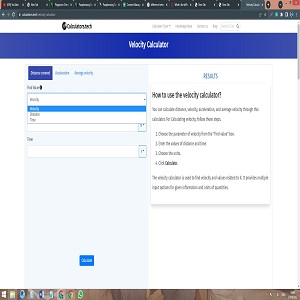
Step 2: Enter the provided data values ​​or required information into the calculator and press the Calculate button.

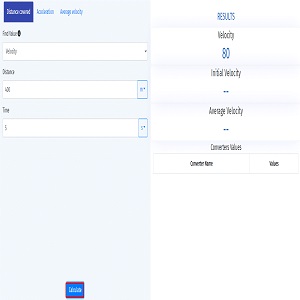
Hence the velocity of vehicle is calculated.

Example 2:

A constructed railway can travel 110 kilometres in 2 hours. What is its normal velocity?

Solution: Manual method

Step 1: write given data values

Distance = d = 120km = 110000m

Time taken = t = 2 hours and 30 minutes = 7200s

Velocity = v =?

Step 2: Write general formula for net force

v = d / t

Step 3: Put the given data values

v = 110000m/ 7200s

v = 15.27m/s

Hence the velocity of built train is 15.27m/s

Summary:

Velocity is just the product of speed and direction of travel. As a result, most of the time, physics is concerned with objects moving in a specified direction. As a result, we need a consistent mechanism for determining how fast an object is moving, in which direction it is heading, where it will be in the next seconds, and so on. As a result, utilising velocity is far more practicable (a quantity we call, Vector Quantity). When a moving item changes direction, its velocity and speed are no longer the same. A velocity calculator enables us to create motion values precisely and intentionally for all of these applications.